| Front Page |
| Aim and Scope |
| Registration |
| Participants |
| Organizers |
| Financial Support |
| Dates and Place |
| Schedule and Courses |
| Hints for Travel |
| Past Editions |
| Contact |
Every course will consist in four sessions of 1 hour and a half, and one session of 1 hour. There will be time for some short junior talks in the afternoon and free time for discussions. Every participant is invited to present a poster.
SCHEDULE:
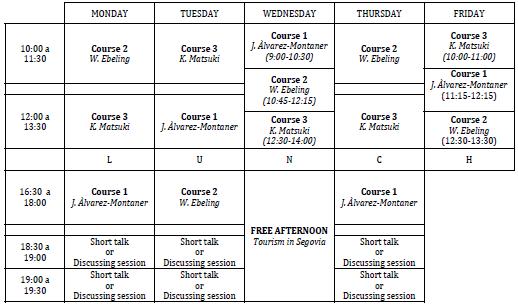
Course 1: Topics on test ideals.
Josep Álvarez-Montaner, Universitat Politècnica de Catalunya
(Spain).
Test ideals and the set of F-jumping numbers they come with provide
some significant invariants of singularities in positive characteristic
that can be understood as an analogue of the multiplier ideals and their
corresponding jumping numbers in characteristic zero.
The aim of this course is to give a gentle introduction to this theory.
Course 2: Introduction to equivariant zeta functions of the monodromy.
Wolfgang Ebeling, Gottfried-Wilhelm Leibniz Universität Hannover
(Germany).
We consider a germ of a complex analytic function in several variables
with an isolated singularity at the origin (simply called singularity).
We introduce an important invariant of such a singularity: the classical
monodromy operator and its zeta function. We show how one can compute
the zeta function of the monodromy from a
resolution of the singularity. We also derive a formula for the monodromy
zeta function of a quasihomogeneous polynomial. We consider a subgroup
$G$ of the group of diagonal symmetries of such a polynomial. We discuss
an equivariant version of the monodromy zeta function which is an element
of the Burnside ring of the group $G$.
Finally we consider a special class of quasihomogeneous polynomials, namely
the so called invertible polynomials. There is a duality between such
polynomials given by the Berglund-Hübsch transpose. This is related
to mirror symmetry. We discuss a duality between the reduced equivariant
monodromy zeta functions of Berglund-Hübsch
dual invertible polynomials which was recently discovered by the speaker
and S. M. Gusein-Zade.
Course 3: Minimal Model Program.
Kenji Matsuki, Purdue University (USA).
The goal of this short course is to introduce the audience to the basic
ideas of the classification theory of (higher dimensional) algebraic varieties
from a view point of the Minimal Model Program (alias Mori’s Program).
The tentative schedule for the lectures is:
- Overview:
- Classification theory of algebraic curves (compact and punctured Riemann surfaces).
- Classification theory of algebraic surfaces (Castelnuovo-Enriques classification).
- Toward classification theory of higher dimensional algebraic varieties via the following three main ingredients:
- Resolution of singularities.
- Minimal Model Program.
- Logarithmic Category.
- General mechanism of the classification scheme:
- Resolution of singularities.
- Minimal Model Program: a flowchart to produce either a minimal model or a Mori fiber space.
- Cone Theorem.
- Contraction Theorem.
- Existence of Flip.
- Termination of Flips.
- Trichotomy of the classification into the three classes:
- Mori fiber spaces: covered by rational curves.
- Calabi-Yau varieties: mysterious.
- Canonically polarized varieties: construction of the moduli space.
- Vanishing Theorems: the main engine for the proofs.
- Kodaira Vanishing Theorem.
- Kawamata-Viehweg Vanishing Theorem: a logarithmic version of Kodaira Vanishing Theorem.
- Proofs of Cone Theorem and Contraction Theorem.
- Inductive structure of the Minimal Model Program: the logarithmic cate- gory provides a natural setting for the induction on dimension.
- Adjunction.
- BCHM proof of Existence of Flips.
- Finite generation of the canonical ring.
- Open problems.
- Termination of Flips.
- Abundance Conjecture.
- Algorithm for Sarkisov Program.